레드 블랙 트리

레드-블랙 트리 (Red-black tree) 란 ?

레드-블랙 트리는 자가 균형 이진 탐색 트리의 한 종류이며, 앞서 살펴본 이진 탐색 트리가 탐색 시 최악의 경우 시간복잡도가 $O(n)$인 부분을 몇 가지 조건을 통해 균형 잡힌 트리로 만들어 최악의 경우에도 탐색 시 $O(log n)$ 을 보장하는 자료 구조이다.

레드-블랙 트리의 조건

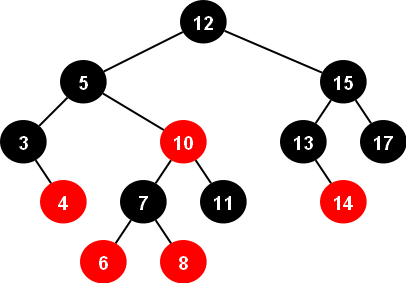
이진 탐색 트리가 가진 조건에서 다음 조건을 만족해야 레드-블랙 트리라고 할 수 있다.

1. 모든 노드는 Red이거나 Black이다.
2. 루트 노드는 Black이다.
3. 모든 리프노드(단말노드)는 Black이다.
4. 노드가 Red이면 그 자식은 Black이다. No Double Red => Red 노드가 연속으로 나올 수 없음
5. 루트노드에서 모든 리프노드까지의 경로에서 만나는 Black노드의 수는 같다.

레드-블랙 트리 삽입 연산

삽입 연산을 통한 레드-블랙 트리를 만들기 전에 알아야 할 사항들이 있다.

• 새로 삽입되는 노드의 색은 무조건 Red 이다.
• Double Red가 발생하지 않기 위해 다음 2가지 전략을 통해 해결한다.
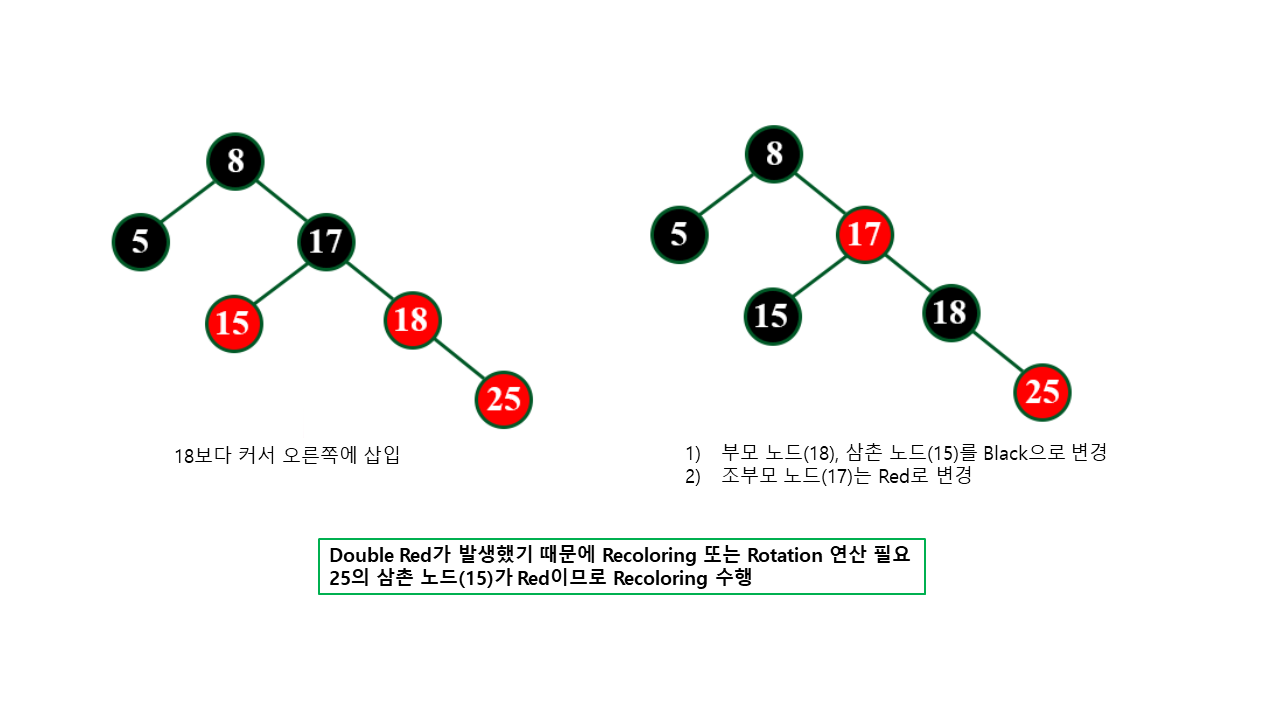
  • Recoloring
    • 새로 삽입된 노드의 삼촌 노드(부모 노드와 형제인 노드) 가 Red인 경우 수행
      • 새로 삽입된 노드의 부모 노드, 삼촌 노드를 Black으로 하고 조부모 노드를 Red로 한다.
      • 조부모 노드가 루트 노드가 아니라면 Double Red가 다시 발생할 수 있다.
      • 위와 같은 상황이 발생하면 그때 다시 Recoloring 또는 Rotation 연산을 수행한다.
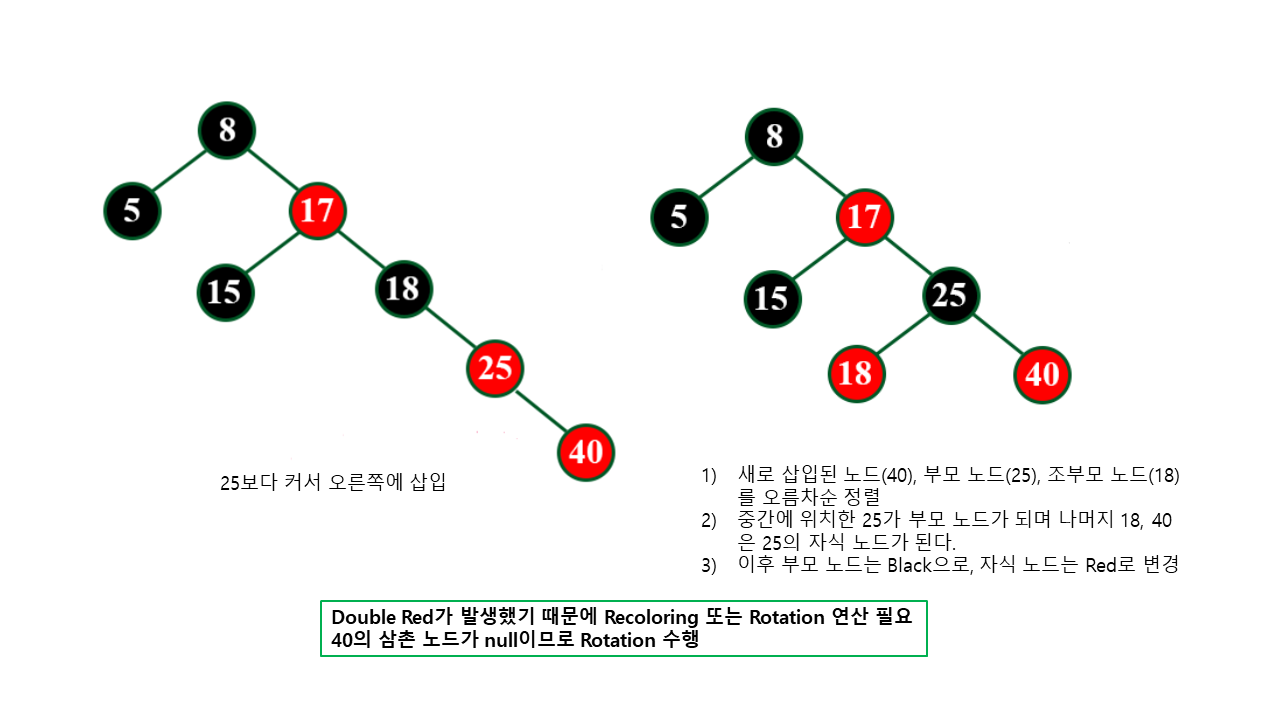
  • Rotation
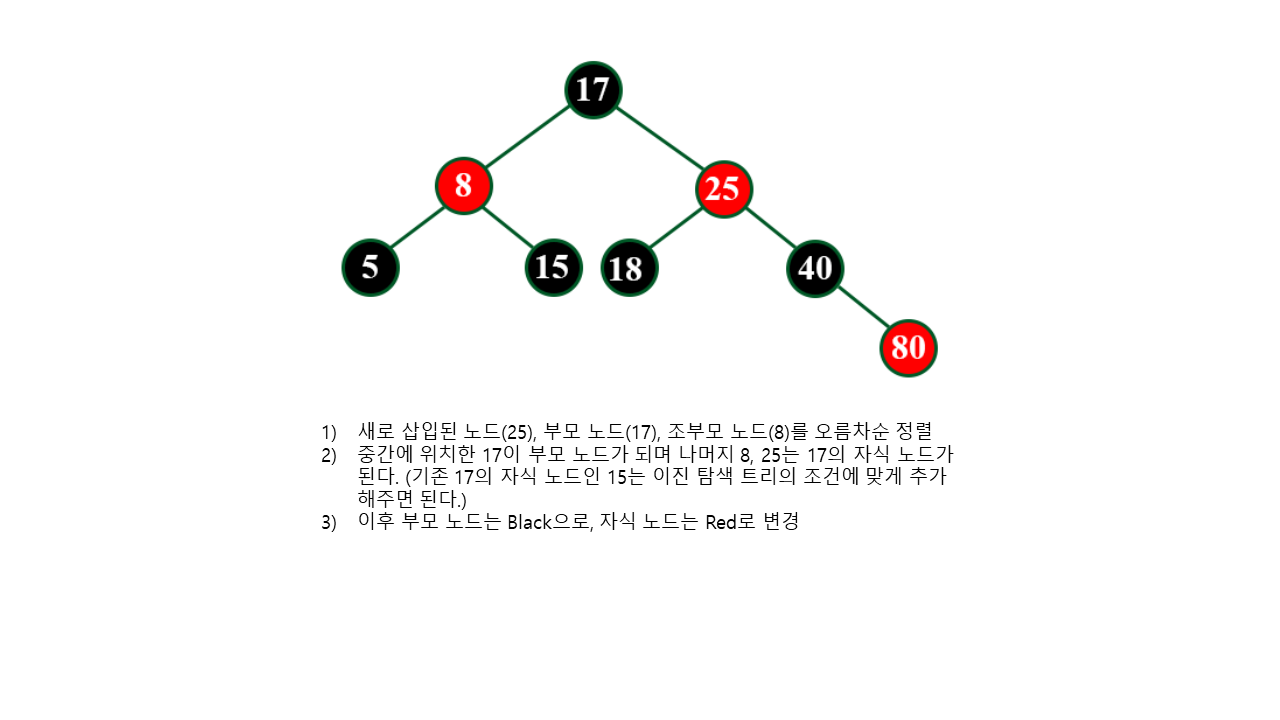
    • 새로 삽입된 노드의 삼촌 노드(부모 노드와 형제인 노드) 가 Black이거나 null인 경우 수행
      • 새로 삽입된 노드, 부모 노드, 조부모 노드를 오름차순으로 정렬한다.
      • 이후, 중간에 위치한 노드를 부모 노드로 하고 나머지 두 노드를 자식 노드로 만든다.
      • 부모 노드를 Black으로 하고, 두 자식들을 Red로 한다.

위 사항들을 숙지하고 레드-블랙 트리 삽입 연산을 진행하면 다음과 같다.

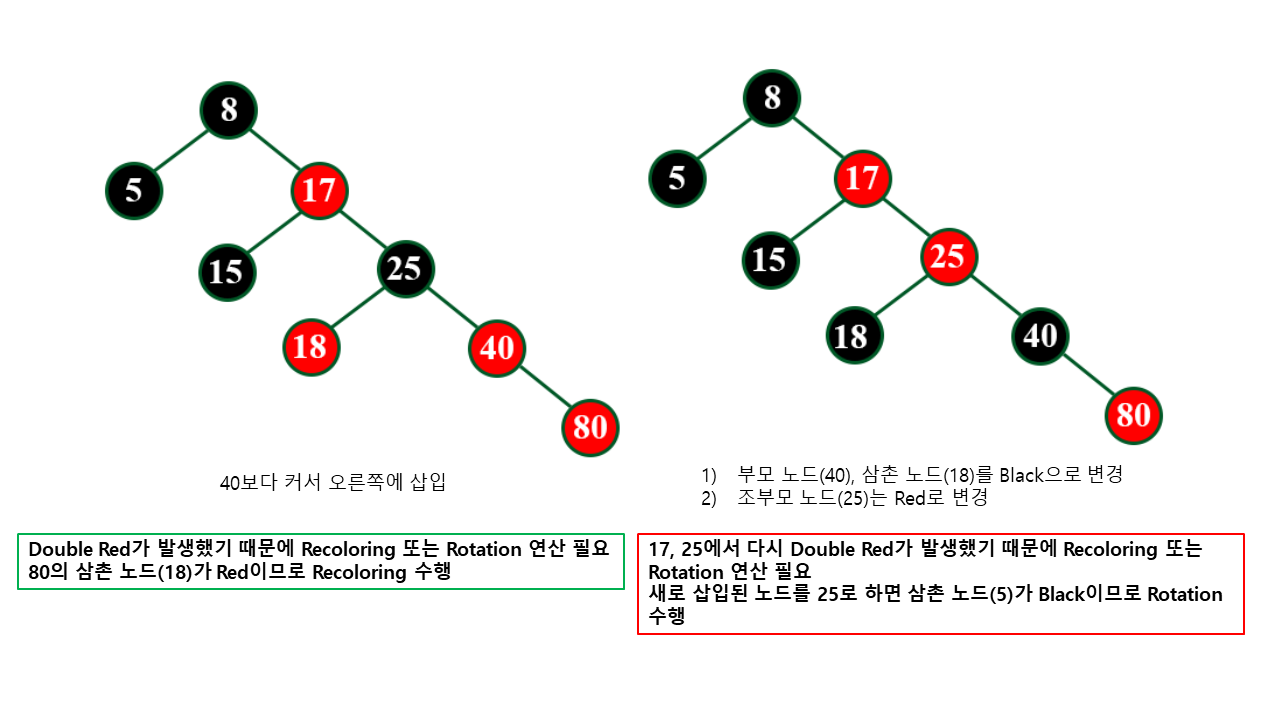
레드-블랙 트리 삭제 연산

• Red 노드를 삭제할 때는 그냥 삭제 연산을 수행하면 된다.
  • Double Red만 아니면 되기 때문이다.
• Black 노드를 삭제할 때는 레드-블랙 트리 조건을 유지하여야 한다.
  • 삽입 연산때 처럼 Rotation을 통해 해결이 가능하다.

레드-블랙 트리 시간복잡도

정의에서 언급한 것 처럼, 레드-블랙 트리는 이진 탐색 트리가 편향되는 모습을 개선한 구조인 자가 균형 이진 트리의 한 종류이다. 그러므로 최악의 경우에도 레드-블랙 트리는의 시간 복잡도는 $O(log n)$이다.

레드-블랙 트리의 장단점

• 장점
  • 최악의 경우에도 일정한 실행 시간을 보장한다.
  • 위와 같은 성능적 장점으로 인해, 실시간 처리와 같은 실행시간이 중요한 경우 유용하게 쓰이며, 일정한 실행 시간을 보장하는 다른 자료구조를 만드는 데에도 유용하다고 한다.
• 단점
  • 이해하기 어려우며 구현이 복잡하다.

나올 수 있는 면접 질문

• 레드-블랙 트리의 정의와 시간복잡도
• 레드-블랙 트리의 삽입 연산 설명

참고

• 레드-블랙 트리 - 위키피디아
• 알고리즘 ) Red-Black Tree - Zedd0202님 블로그
• RedBlack Tree에 대해 - Nesoy님 블로그
• RB tree - Ratsgo님 블로그
• Red - Black Tree Datastructure - btechsmartclass

기여자

_{Junho Moon}
📦