이진탐색트리
1. 기술 정의
이진탐색트리란 이진탐색 (Binary Search)와 연결리스트(Linked List)를 결합한 자료구조의 일종이다.
| 이진 탐색 | 연결 리스트 | |
|---|---|---|
| 장점 | 탐색에 소요되는 시간복잡도가 O(logN) 로 빠르다 | 삽입과 삭제에 걸리는 시간 복잡도가 O(1)로 빠르다 |
| 단점 | 삽입과 삭제가 불가능하다 | 탐색의 시간 복잡도가 O(N) 이다 |
위와 같은 이진 탐색과 연결리스트의 장점을 고안하기 위해 만들어졌으며, 이진 탐색의 효율적인 탐색 능력을 유지하면서도 빈번한 자료 입력과 삭제가 가능하기 위해 사용된다.
2. 기술 내용
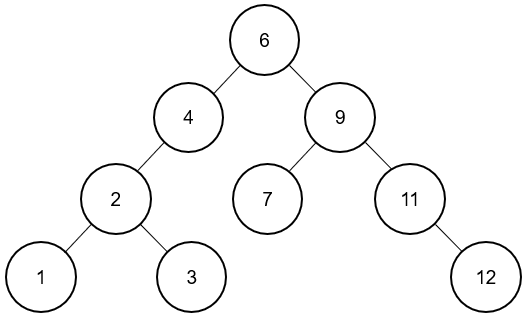
이진탐색트리는 이진트리의 일종으로 다음과 같은 규칙으로 구성한다.
- 모든 노드는 유일한 키를 갖는다 (중복된 노드가 없어야 한다)
- 각 노드의 왼쪽 서브 트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어져 있다.
- 각 노드의 오른쪽 서브 트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어져 있다.
- 각 노드의 왼쪽, 오른쪽 서브트리 또한 이진탐색트리로 구성한다.
다음은 이진탐색트리가 가진 특징이다.
탐색의 시간 복잡도는 트리의 높이를 h라고 할 때
O(h)이다.위와 같은 편향 트리의 경우 탐색에 O(N)의 시간이 소요된다.
이진탐색 트리의 순회는 중위 순회 (in order) 방식이다. (왼쪽 - 루트 - 오른쪽)
중위 순회: 4, 7, 16, 20, 37, 38, 43 (중위 순회 방식으로 정렬된 순서를 얻을 수 있다)
이진탐색트리의 삽입 연산은 루트노드에서 탐색을 시작해 서브트리가 없는 잎새 노드에서 이뤄진다.
이진탐색트리의 삭제 연산은 세가지 케이스로 나눠서 연산한다.
자식 노드가 없는 경우 -> 삭제할 노드를 그냥 없앤다
자식 노드가 하나 있는 경우 -> 삭제할 노드의 자식을 올린다
자식 노드가 두 개 있는 경우 -> 오른쪽 서브 트리에서 가장 작은 값이나 왼쪽 서브 트리에서 가장 큰 값을 올린다.
자식 노드가 두 개인 경우 오른쪽 서브트리와 왼쪽 서브트리 중 어느 것을 선택해야 하나요?
오른쪽 서브트리와 왼쪽 서브트리를 정하는 규칙은 따로 정해져있지 않으며 두 방식에 차이가 있지 않습니다. 따라서 구현자가 두 방식 중에 자유롭게 선택해 규칙을 정할 수 있습니다.