트라이
트라이란?
문자열 집합에서 어느 한 개의 문자열을 탐색하는 알고리즘은 무엇이 있을까? 최대 길이가 m인 문자열 n개의 집합이 있다고 가정해 보자.
가장 간단하지만 시간복잡도가 높은 방식 첫번째는 무작정 순회를 돌며 찾는 방식인 brute force이다. 최대 길이가 m인 문자열 n개의 집합에서, 원하는 문자열이 있는지 찾는다면 비교횟수는 O(mn)이 된다.
이를 좀더 개선하는 방식은 이진 탐색을 활용하면 좀더 낮은 시간복잡도를 갖게 된다. 이진 탐색을 사용하면 O(mlogn)으로 단축 시킬 수 있지만, 정렬 과정 자체에 O(nmlogn)의 시간이 걸려서 이 또한 비효율적인 방식이라고 볼 수 있다.
이를 모두 개선하기 위한 문자열 집합 검색법이 바로 Trie라는 자료구조이다. 이를 Trie 알고리즘이 아닌 자료구조라는 말을 사용하는 이유는 트라이가 갖는 트리 종류를 보고 부르는 것인데 이는 잠시 후에 알아보도록 하고 트라이의 기원부터 살펴보도록 하자.
트라이의 개념은 1959년 René de la Briandais가 처음 설명하였고 처음에는 tri라고 불렸다가 tree의 이름과 헷갈려서 나중에 에드워드 프레드킨이 trie(트라이)라는 이름으로 명명하였다.
트라이 자료구조
이제 트라이가 왜 자료구조인지, 그 트라이 자료구조에 대해 아래 그림과 함께 살펴보도록 하자.
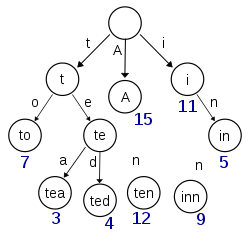
{"A", "to", "tea", "ted", "ten", "i", "in", "inn"} 다음과 같은 문자열 집합이 있다고 해보자. 이 문자열을 트리형태로 한글자씩 따서 그 깊이만큼 만들면 위와 같은 트리구조를 형성한다.
트라이 자료구조를 만들 때 삽입은 O(m)의 시간복잡도로 주어진 문자열을 트라이 자료구조로 만들 수 있다. 또한 검색의 경우에도 O(m)의 시간복잡도로 검색이 가능하다. 이러한 삽입과 검색의 연산을 파이썬 구현으로 확인해 보자.
트라이의 구현
class Node(object):
def __init__(self, key, data=None):
self.key = key
self.data = data
self.children = {}
class Trie(object):
def __init__(self):
self.head = Node(None)
# 삽입 : head노드 부터 시작하여 문자열의 길이 만큼 돌며 자리를 찾는다.
# 시간복잡도 O(M), M : string의 길이
def insert(self, string):
cur_node = self.head
for char in string:
# 자식노드에 해당 문자가 없으면 해당 문자로 자식노드를 만들어준다.
if char not in cur_node.children:
cur_node.children[char] = Node(char)
cur_node = cur_node.children[char]
# 마지막 노드까지 온 후 데이터를 string으로 해준다.
cur_node.data = string
# 검색
# 시간복잡도 O(M), M : string의 길이
def search(self, string):
cur_node = self.head
for char in string:
if char in cur_node.children:
cur_node = cur_node.children[char]
else:
return False
# 탐색이 끝난 후
# 해당 노드의 data가 있다면 문자가 포함되어 있다는 뜻
if cur_node.data != None:
return True
트라이 특징
앞서 말한대로 트라이는 문자길이 m을 갖는 문자열을 O(m)의 시간으로 트라이 자료구조로 만들 수 있고, 탐색할 때도 마찬가지로 O(m)의 시간으로 탐색이 가능하다.
하지만 트라이는 이러한 자료구조를 구성하는 공간복잡도가 엄청나게 많이 필요하게 된다. 문자열이라면 a~z 총 26개의 포인터 배열을 1 depth마다 갖게 될 수도 있기 때문이다. 이러한 특성 때문에 트라이의 공간복잡도는 0(포인터크기 * 포인터 배열 개수 * 트라이에 존재하는 총 노드의 개수)가 된다.
이를 해결하기 위해 비트 트라이, 트라이 압축, 외부 기억장치 트라이등의 다양한 구현전략이 등장하게 되었다. 이러한 구현전략에 좀 더 자세히 알고 싶다면 여기에서 한번 확인하기 바란다.
하지만 일반적인 알고리즘 풀이에서는 이러한 구현전략들을 사용하기가 어렵기 때문에, 트라이를 사용할 때는 꼭 문자열 집합중 문자열 1개의 최대길이가 몇까지 가능한지를 확인하고 그 길이가 작다면 트라이를 사용하는 것을 추천하는 바이다.
트라이 사용
트라이는 자동완성, 정렬, 전문 검색등에서 사용이 가능하다.
- 자동완성 : 주어진 접두사를 가진 리스트를 반환하는데 활용할 수 있다.
- 정렬 : 키 집합으로 하위노드가 정렬된 트라이를 만들면 집합 전체를 사전순으로 정렬할 수 있다.
- 전문 검색 : 트라이의 특수한 형태로써 접미사 트리(suffix tree)라고 불리는 것은 빠른 전문(full-text) 검색에 활용하기 위해 모든 접미사를 색인하는데 이용할 수 있다.
트라이 관련 문제와 관련 주제
- 백준 트라이 분류중 풀고 싶은 문제를 풀어보도록 하자.
문자열 관련 알고리즘은 많은데 문자열 알고리즘 - 나무위키사이트에 궁금하다면 들어 가보는 것도 좋을 것 같다.
나올 수 있는 면접 질문
- 트라이 자료구조란 무엇인가요?
- 트라이의 시간복잡도는 어떻게 되나요?
- 트라이 자료구조의 삽입과정과 검색과정을 설명해주세요.
- 트라이의 단점은 무엇인가요?
참고 url
기여자
Kyun Heo
📦