Skip to main content

트리

Tree​

트리의 개념​

  • 트리는 노드로 이루어진 자료 구조
    • 트리는 하나의 루트 노드를 갖는다
    • 루트 노드는 0개 이상의 자식 노드를 갖고 있다.
    • 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
  • 노드들과 노드들은 연결하는 간선들로 구성되어 있다.
    • 트리에는 사이클(cycle)이 존재할 수 없다.
    • 노드들은 특정 순서로 나열될 수도 있고 그럴 수 없을 수도 있다.
    • 각 노드는 부모 노드로의 연결이 있을 수도 있고 없을 수도 있다.
    • 각 노드는 어떤 자료형으로도 표현 가능하다.
  • 비선형 자료구조로 계층적 관계를 표현한다.
  • 그래프의 한 종류
    • 사이클(cycle)이 없는 하나의 연결 그래프(Connected Graph)
    • 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류이다.

트리의 특징​

  • 그래프의 한 종류이다. '최소 연결 트리' 라고도 불린다.
  • 트리는 계층 모델이다
  • 트리는 DAG(방향성이 있는 비순환 그래프)의 한 종류이다.
    • loop나 circuit이 없다.
    • 즉, 사이클이 없다
  • 노드가 N개인 트리는 항상 N-1개의 간선(edge)를 가진다.
    • 즉, 간선은 항상 (정점의 개수 -1)만큼을 가진다.
  • 루트에서 어떤 노드로 가는 경로는 유일하다.
    • 임이의 두 노드 간의 경로도 유일하다. 즉, 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
  • 한 개의 루트 노드만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다.
    • 부모-자식 관계이므로 흐름은 top-bottom 아니면 bottom-top으로 이루어진다.
  • 순회는 Pre-order, In-order, Post-order로 이루어진다. 이 3가지 모두 DFS/BFS 안에 있다.
  • 트리는 이진트리, 이진 탐색트리, 균형트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등이 있다.

Mininum Spanning Tree(최소 신장 트리)​

Spanning Tree란 그래프 내의 모든 정점을 포함하는 트리입니다.

  • Spanning Tree는 그래프의 최소 연결 부분 그래프라는 특징을 가지고 있다.
  • 최소연결 = 간선의 수가 가장 적다
  • 하나의 그래프에는 많은 신장 트리가 존재할 수 있다.
  • Spanning Tree는 트리의 특수한 형태이므로 모든 정점들이 연결되어 있어야하고 사이클을 포함해서는 안된다.
  • MST=최소 신장 트리, MST는 간선에 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것을 말한다.

mst_graph

트리의 용어​

tree

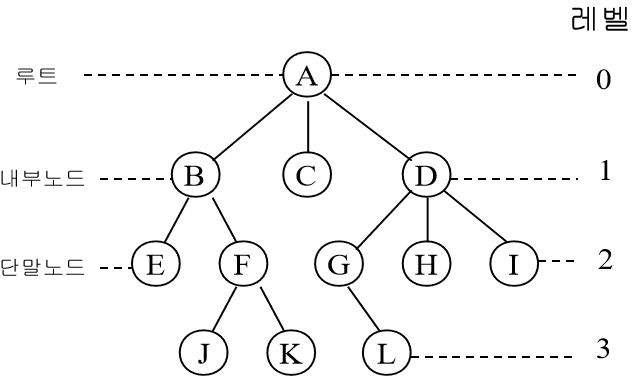
  • 노드의 차수- 한 노드가 가진 서브트리의 수
    • A의 차수: 3, B의 차수: 2, C의 차수: 0
  • 리프노드(단말,터미널) - 차수가 0인 노드
    • 리프노드: E, J, K, L, H, I, C
  • 자식노드- 노드에 연결된 서브트리의 루트노드들
    • A의 자식노드: B, C, D
  • 부모노드- 노드에 연결된 한단계 상위 레벨 노드
    • I의 부모노드: D
  • 형제 노드- 부모가 같은 노드
    • G, H, I는 형제노드
  • 트리의 차수- 트리노드들의 차수중 최대 차수
    • 트리의 차수:3
  • 트리의 깊이(높이)- 트리의 최대 레벨
    • 트리의 깊이: 3

트리의 종류​

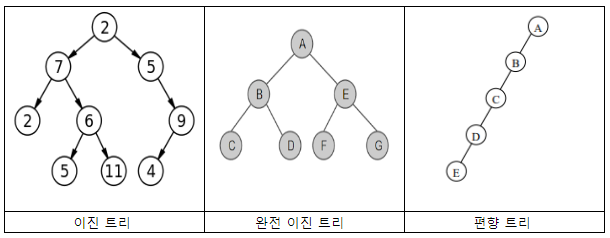
tree_table

이진트리(Binary tree)​

  • 이진트리란 자식노드가 최대 두 개인 노드들로 구성된 트리입니다. 이진트리에는 정이진트리, 완전이진트리, 균형이진트리 등이 있다.

트리의 순회(Tree Traverse)​

트리의 순회에는 크게 3가지의 순회 방식이 있다.

  • 전위 순회(preorder traverse): 루트를 먼저 방문
  • 중위 순회(inorder traverse): 왼쪽 하위 트리를 방문 후 루트를 방문
  • 후위 순회(postorder traverse): 하위 트리 모두 방문 후 루트를 방문

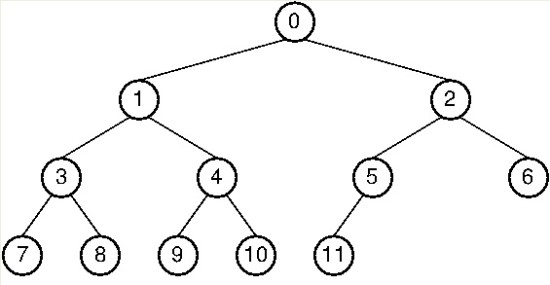
tree_example

전위순회: 0->1->3->7->8->4->9->10->2->5->11->6

중위순회: 7->3->8->1->9->4->10->0->11->5->2->6

후위순회: 7->8->3->9->10->4->1->11->5->6->2->0

위와같은 순서로 각 순회를 진행하게 된다.

이진트리의 시간복잡도​

사실 이진트리의 시간복잡도는 순회만 했을 때 기준 O(N)입니다.

만약 탐색에 대한 기준이 있다면 이를 이진탐색트리(binary search tree)라고 하는데 이럴 경우 트리의 높이만큼의

시간이 소요되므로 탐색의 시간복잡도는 O(h -> 트리의 높이)이다.

따라서 균형이 잡힌 이진트리의 경우 O(logN)의 시간복잡도를 가지게된다.

그래프와 트리의 차이​

graph-vs-tree

관련 면접 질문​

  • BST(Binary Search Tree)와 Binary Tree에 대해서 설명하세요.
  • 트리와 그래프의 차이점에 대해서 설명하세요.
  • 트리를 활용했을 때 장점이 무엇인가요?
참고자료​

https://galid1.tistory.com/174

https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html

https://kingpodo.tistory.com/27

https://velog.io/@humblechoi/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EB%A9%B4%EC%A0%91%EC%A7%88%EB%AC%B8-%EB%AA%A8%EC%9D%8C

기여자​


Youngwoo Kim
📦