Skip to main content

B-Tree & B+Tree

1. B-Tree란?​

B-Tree는 자식 노드의 개수가 2개 이상인 트리를 말한다. 이진트리가 자식 노드가 최대 2개인 트리를 말하는 것인데, 이 이진트리를 확장해서 더 많은 수의 자식을 가질 수 있게 일반화 시킨 것이 B-Tree이다.

2. B-Tree의 구조​

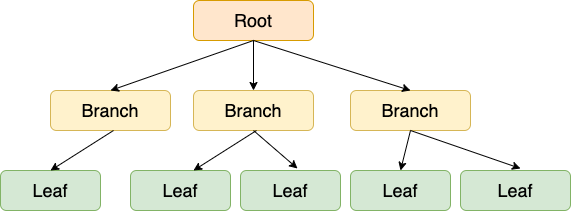
TreeStructure

그림의 네모 칸 하나 하나를 '노드' 라고 하며, 가장 상단의 노드를 '루트 노드(Root Node)', 중간 노드를 '브랜치 노드(Branch Node)', 가장 하단의 노드를 '리프 노드(Leaf Node)' 라고 한다.

안의 구조를 자세히 살펴보면 다음과 같다.

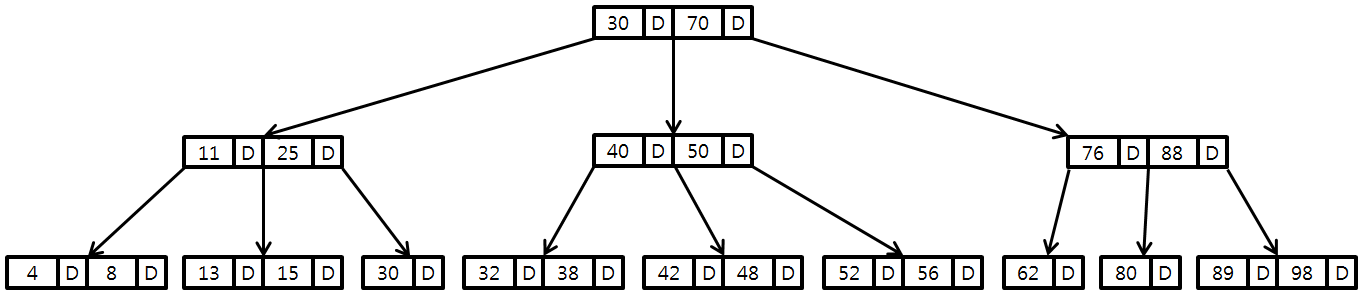
B-TreeStructure

위 그림에서 보듯이, 노드당 데이터를 2개 이상 가질 수 있으며 자식 노드를 자신의 데이터 수 이상으로 가질 수 있다. 즉, 노드의 데이터가 N개이면, 자식 수는 N+1개가 된다.

여기서 노드당 최대 M개의 자식노드를 가질 때, M차 B트리 라고 한다.

3. B-Tree의 규칙​

  • 노드의 자료수가 N이면, 자식 수는 N+1이어야 함
  • 각 노드의 자료는 정렬된 상태여야함 ( 1, 3, 5 처럼 )
  • 루트 노드는 적어도 2개 이상의 자식을 가져야함
  • 루트 노드를 제외한 모든 노드는 적어도 M/2개의 자료를 가지고 있어야함
  • 외부 노드(Leaf Node)로 가는 경로의 길이는 모두 같음.
  • 입력 자료는 중복 될 수 없음
  • 이진트리와 같이 노드 데이터보다 작은값은 왼쪽에, 큰 값은 오른쪽에 위치한다.

4. B-Tree의 삽입, 삭제​

① B-Tree의 삽입 연산

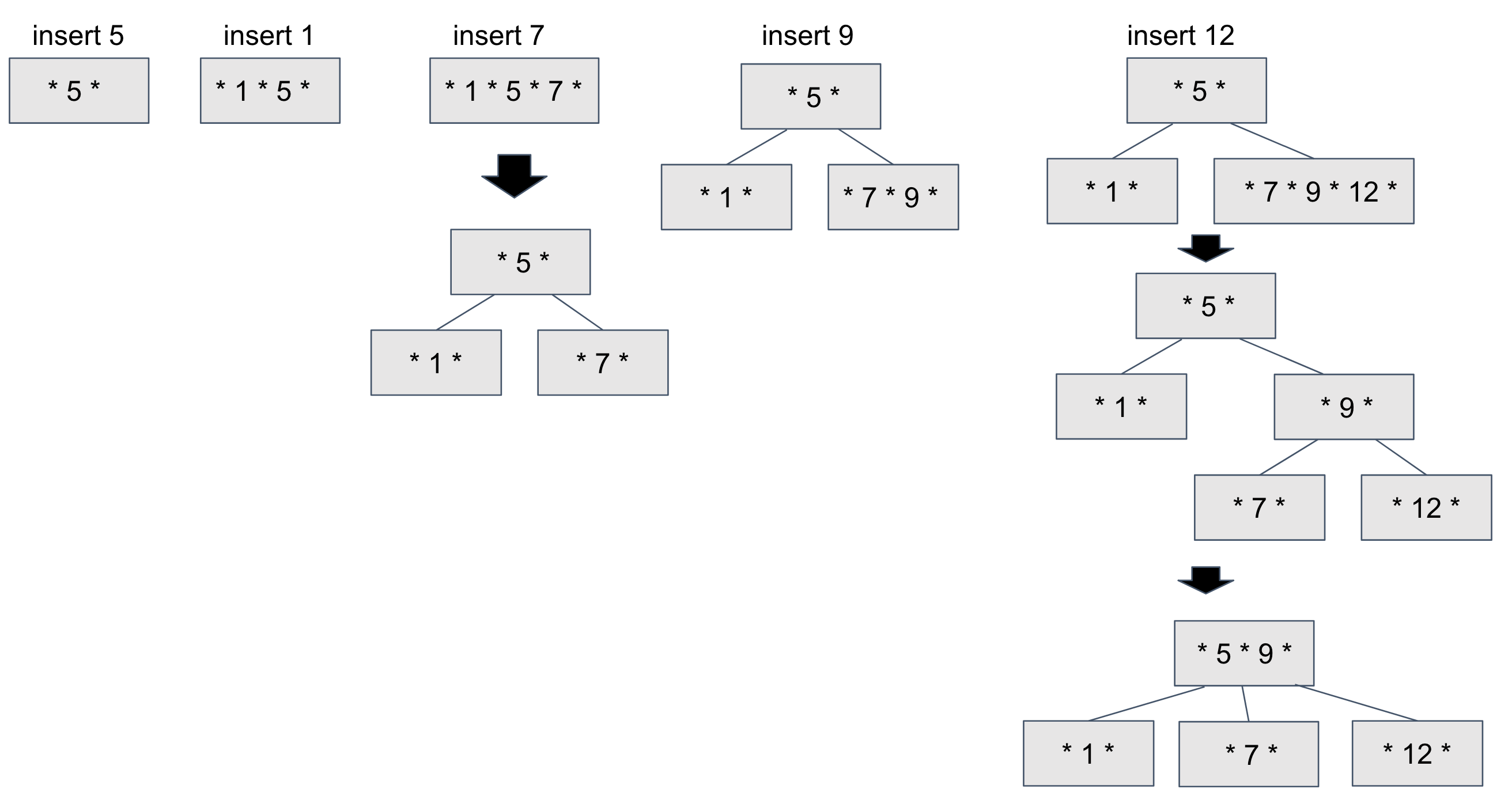
B-TreeInsertion

  1. 데이터를 탐색해 해당하는 Leaf 노드에 데이터 삽입

  2. Leaf 노드 데이터가 가득 차 있으면 노드를 분리하여 서브트리 구성 ( 위의 insert 7 참고 )

  3. 분리한 서브트리가 B-Tree 규칙에 맞지 않는다면 부모 노드로 올라가 merge

    (insert 12에서 [9, 7, 12] 를 서브트리로 분리하였지만 B-Tree의 조건인 "Leaf노드가 모두 같은 레벨에 존재" 를 만족시키지 못했으므로 root로 merge)

② B-Tree의 삭제 연산

전체적인 과정은 다음과 같다.

  1. 삭제할 키가 있는 노드 검색
  2. 키 삭제
  3. 필요한 경우, 트리 균형을 위한 조정

자세한 과정을 예시로 설명하면 다음과 같다. ( 리프노드인 1 삭제 )

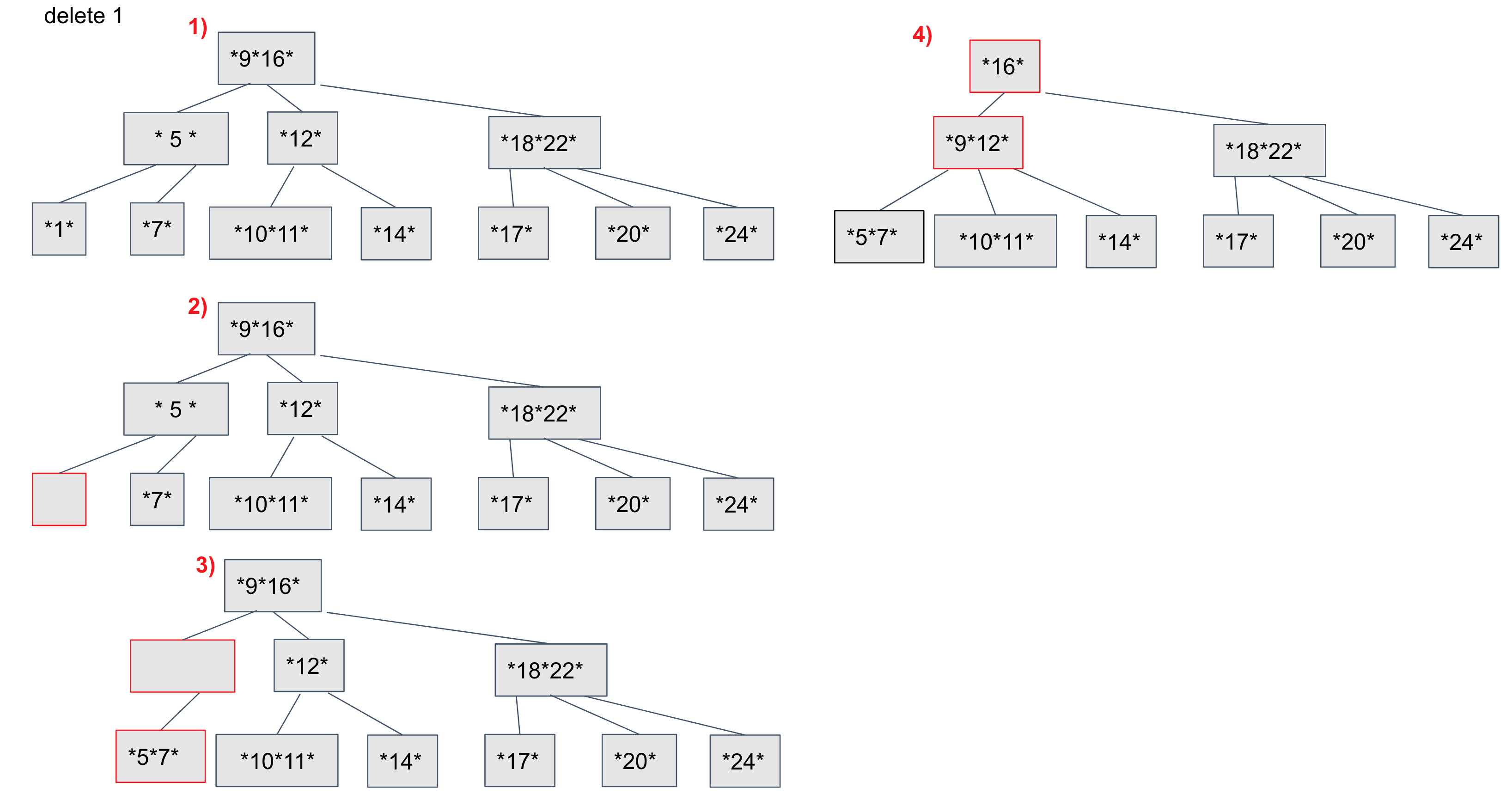
B-TreeDelete

  1. 1을 찾아 루트부터 탐색한다

  2. 1을 삭제한다

  3. 트리의 균형이 깨져 조정 작업을 진행한다

    3-1) 1의 부모노드(5)를 가져온다

    3-2) 형제 노드(7)와 merge한다

    3-3) 한 단계 더 올라가 부모노드중 한 값을(9) 자식 노드로 값을 가져온다

    3-4) 형제 노드(12)와 merge한다.

    3-3,4 과정을 root노드까지 올라가며 균형이 맞을 때 까지 반복한다.

리프노드가 아닌 노드를 삭제할 때의 과정은 다음과 같다 (이너 노드인 18 삭제 )

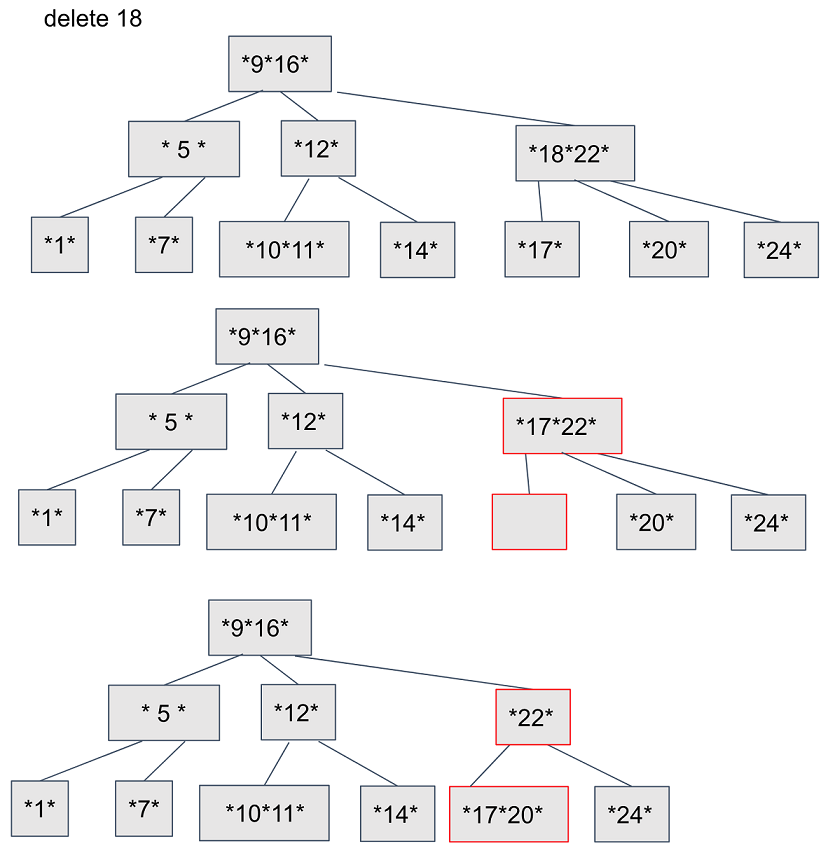
B-TreeDelete2

  1. 18을 찾아 루트부터 탐색한다

  2. 18을 삭제한다

  3. 트리의 균형이 깨져 조정 작업을 진행한다

    3-1) 왼쪽 서브트리의 최댓값인 17을 가져온다

    3-2) 부모노드(17, 22)중 적절한 값(17)을 자식노드로 가져온다

    3-3) 형제노드(20)와 merge 한다.

    3-2,3 과정을 root노드까지 올라가며 균형이 맞을 때 까지 반복한다.

5. B+Tree란?​

B-Tree의 확장개념으로, 데이터의 빠른 접근을 위해 인덱스 역할만 하는 비단말 노드(Not Leaf)가 추가로 존재한다.

브랜치 노드에는 노드를 찾아갈 수 있는 Key만 담아두고 리프 노드에 Key와 Data가 존재한다. 그리고 리프 노드끼리는 LinkedList로 연결되어 있다.

6. B+Tree의 구조​

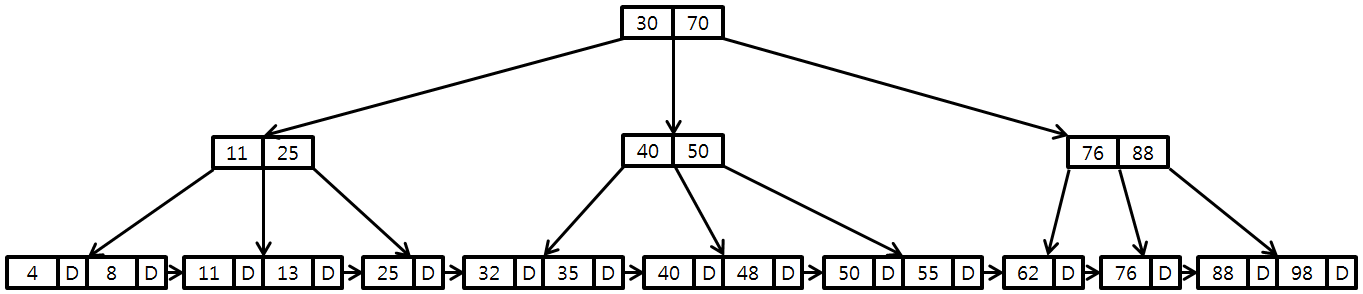
B+TreeStructure

위의 그림처럼 InnerNode는 LeafNode의 데이터를 찾아가는 데에만 쓰이며, LeafNode끼리는 LinkedList로 연결되어 있다.

7. B+Tree와 B-Tree의 차이점​

  • B-Tree는 모든 노드에 데이터가 저장됨
  • B+Tree는 Leaf에만 데이터 저장. 나머지 노드에는 Key만 저장됨 ( 메모리 활용에 효율적 )
  • B-Tree는 탐색시, 최상의 경우엔 루트에서 끝날 수 있지만,
  • B+Tree는 최상의 경우에도 일단 Leaf로 내려가야 함
  • B-Tree는 순차 탐색시에도 매번 루트에서 탐색을 시작하지만,
  • B+Tree는 순차탐색 시 LinkedList를 통해 빠르게 이어나갈 수 있음 (범위 탐색과 풀스캔에 유리)

8. 면접 시 예상 질문​

  • B-Tree의 시간복잡도가 O(logN)인 이유는 무엇인가요?
  • B-Tree의 사용 예시는 무엇이 있을까요?
  • B+Tree가 B-Tree와 비교하여 장단점을 한가지씩 말해보세요

9. 참고​

10. 기여자​


HongEunho
📦