동적 계획법
동적 계획법이란?
동적 계획법 (Dynamic Programming, DP)는 큰 문제를 작은 문제로 나누어서 푸는 방식의 알고리즘이다. 특정 범위의 값을 구하기 위해서, 다른 범위의 값을 활용해 효율적으로 값을 구하는 방식을 사용한다.
동적 계획법의 조건
동적 계획법은 처음 주어진 문제를 작은 문제로 나눠서 답을 구하는 점에서 분할 정복과 비슷하지만, 동적 계획법은 분할 정복과 달리 문제와 답이 중복 될 수 있다는 특징이 있다.
위와 같은 특징 때문에 동적 계획법은 항상 사용할 수 없으며, 다음과 같은 조건을 만족할 때 사용할 수 있다.
1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
메모이제이션이란?
동적 계획법에서는 동일한 문제는 오직 한 번만 풀어야 한다.
동적 계획법의 조건 (작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다) 에 따르면 같은 문제는 풀이 할 때마다 정답이 같으므로, 그 정답 값을 메모리에 저장해야 한다.
이렇게 정답 값을 메모하는 것은 코드에서 배열에 저장하는 것으로 볼 수 있고, 이것을 메모이제이션 이라고 한다.
피보나치 함수로 보는 메모이제이션
피보나치 함수를 예시로 동적계획법과 메모이제이션에 대해 이해해보자.
def fibonacci(n):
if n <= 2:
return n
return fibonacci(n-1) + fibonacci(n-2)
위 코드는 python을 활용해 재귀적으로 구현한 피보나치 함수이다.
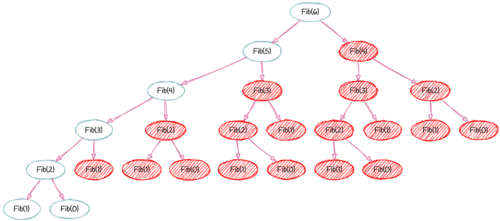
위 함수를 통해 fibonacci(5)를 호출 할 경우 다음과 같다.
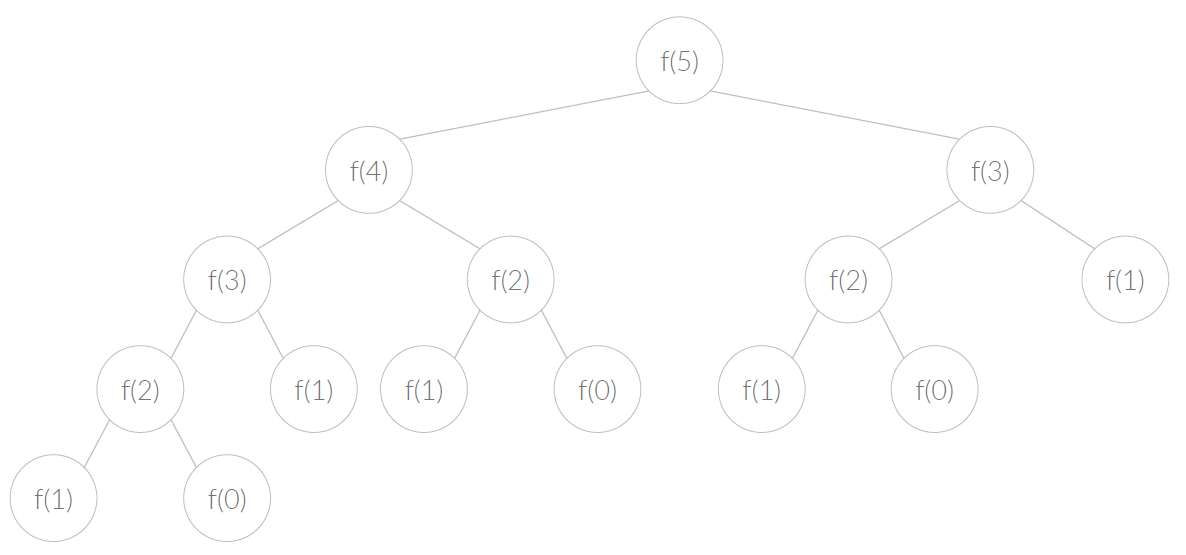
이미지 출처 : https://velog.io/@polynomeer/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming
이 때 f(3)은 겹치는 부분 문제이므로 메모이제이션을 활용해서 값을 저장하는 과정이 필요하다.
# 메모이제이션을 위한 리스트 (임의의 100개)
memo = [0] * 100
def fibonacci(n):
if n <= 2:
return n
# 메모이제이션 된 값이면 재귀 생략후 memo값 반환
if memo[n] != 0:
return memo[n]
memo[n] = fibonacci(n-1) + fibonacci(n-2)
위와 같이 메모이제이션을 활용한다면 중복된 값을 활용해서 문제를 해결 할 수 있을 것이다.

이미지 출처 : https://velog.io/@polynomeer/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming
동적 계획법 구현 방식
동접 계획법을 구성하는 방식은 top-down 과 Bottom-up 두 가지 방식이 있다.
top-down
top-down 방식은 큰 문제 -> 작은 문제 로 쪼개면서 문제를 해결하는 방식이다. 재귀로 구현되며 다음과 같은 과정으로 구현한다.
1. 큰 문제를 작은 문제로 나눈다
2. 작은 문제를 푼다
3. 작은 문제를 푼 뒤에, 큰 문제를 푼다
피보나치를 예시로 들면 Top-down 방식은 메모이제이션에서 살펴봤던 예제와 같다.
# 메모이제이션을 위한 리스트 (임의의 100개)
memo = [0] * 100
def fibonacci(n):
if n <= 2:
return n
# 메모이제이션 된 값이면 재귀 생략후 memo값 반환
if memo[n] != 0:
return memo[n]
memo[n] = fibonacci(n-1) + fibonacci(n-2)
python에서 top-down 방식을 조심해야 하는 이유
python에서는 재귀 함수 깊이가 최대 1000이므로 top-down 방식으로 구현 시 재귀 오버헤드가 발생할 수 있다.
이 경우 sys 라이브러리를 사용하여 재귀 제한을 완화할 수 있으나, 가능하다면 top-down 대신 bottom-up 방식으로 구현하는 것이 권장된다
bottom-up
bottom-up 방식은 작은 문제부터 차례대로 문제를 해결하는 방식이다. 반복문로 구현되며 다음과 같은 과정으로 구현한다.
1. 문제를 크기가 작은 문제부터 차례대로 푼다
2. 문제의 크기를 조금씩 크게 만들면서 문제를 푼다
3. 작은 문제를 풀면서 왔기 떄문에 큰 문제를 바로 풀 수 있다
4. 반복하면서 가장 큰 문제까지 푼다
피보나치 함수를 bottom-up 방식으로 구현한다면 다음과 같다.
# 메모이제이션을 위한 리스트 (임의의 100개)
memo = [0] * 100
def fibonacci(n):
d[0] = 0
d[1] = 1
# 2부터 n까지 반복
for i in range(2,n+1):
memo[i] = fibonacci(i-1) + fibonacci(i-2)
방식별 장단점
top-down
- 장점
- 구현이 간단하다
- 필요한 경우만 계산하고, 계산이 필요하지 않으면 생략한다
- 단점
- 스택의 공간이 부족할 수 있다
- 시간 복잡도와 공간 복잡도를 추론하기 어렵다
- 재귀 오버헤드 문제가 있을 수 있다
bottom-up
- 장점
- 공간 최적화가 가능하다
- 재귀 오버헤드가 없다
- 시간 복잡도와 공간 복잡도의 추론이 쉽다
- 단점
- 반복문에 들어가므로 모든 상태를 계산해야 한다
- 일반적으로 구현하기 더 어렵다
대표적인 DP 문제
면접에 나올 수 있는 질문
Q. 동적계획법의 두 가지 방식은?
Q. 동적계획법과 분할 정복의 차이점은?
참고
기여자
Jongminfire
📦