Skip to main content

다익스트라

다익스트라 (Dijkstra)​

다익스트라 알고리즘은 최단경로를 찾기 위한 알고리즘이며, 특정 정점에서 다른 모든 정점으로 가는 최단 경로를 구할 수 있다. 단, 음의 간선이 없을 때 정상적으로 동작하며, 현실 세계에 사용하기 적합한 알고리즘이다. 이후에 로직을 살펴보겠지만, 다익스트라는 매 순간에 최선의 선택을 하는 그리디 알고리즘으로 분류할 수 있다.

다익스트라 기본 로직​

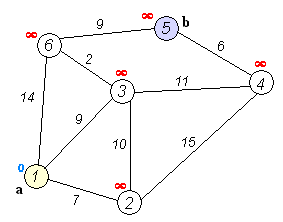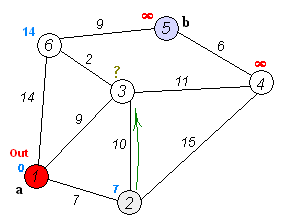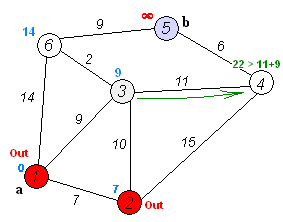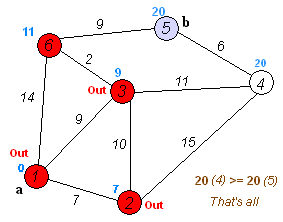
다익스트라 알고리즘의 기본 로직은 다음과 같다.

  1. 출발 지점 설정
  2. 최단 거리를 저장하는 테이블을 무한대로 초기화
  3. 출발 지점과 인접한 노드와의 거리 갱신
  4. 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택
  5. 위에서 선택한 노드를 거쳐서 다른 노드로 가는 비용을 계산하여 테이블 갱신
  6. 4번과 5번 과정을 반복
    

다익스트라 알고리즘 구현 (java)​

기본적인 다익스트라 알고리즘은 방문하지 않은 노드 중에서 가장 거리가 짧은 노드를 선택하기 위해 1차원 테이블의 모든 원소를 순차적으로 탐색해야 한다. 이렇게 되면 V번에 걸쳐서 선형 탐색을 진행해야 하며, 전체적인 시간 복잡도는 O(V2)O(V^2)가 된다. 이런 성능적인 단점을 개선하기 위하여 보통 다익스트라 알고리즘을 구현할 때, 방문하지 않은 노드 중에서 가장 거리가 짧은 노드를 선택할 때 우선순위 큐를 사용하게 된다. 우선순위 큐를 사용할 경우 시간복잡도는 O(ElogV)O(ElogV) 가 된다.

import java.util.*;

class Node implements Comparable<Node> {

    private int index;
    private int distance;

    public Node(int index, int distance) {
        this.index = index;
        this.distance = distance;
    }

    public int getIndex() {
        return this.index;
    }

    public int getDistance() {
        return this.distance;
    }

    // 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
    @Override
    public int compareTo(Node other) {
        if (this.distance < other.distance) {
            return -1;
        }
        return 1;
    }
}

public class Main {

    public static final int INF = (int) 1e9; // 무한을 의미하는 값으로 10억을 설정
    // 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
    // 노드의 개수는 최대 100,000개라고 가정
    public static int n, m, start;
    // 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
    public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
    // 최단 거리 테이블 만들기
    public static int[] d = new int[100001];

    public static void dijkstra(int start) {
        PriorityQueue<Node> pq = new PriorityQueue<>();
        // 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
        pq.offer(new Node(start, 0));
        d[start] = 0;
        while(!pq.isEmpty()) { // 큐가 비어있지 않다면
            // 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
            Node node = pq.poll();
            int dist = node.getDistance(); // 현재 노드까지의 비용
            int now = node.getIndex(); // 현재 노드
            // 현재 노드가 이미 처리된 적이 있는 노드라면 무시
            if (d[now] < dist) continue;
            // 현재 노드와 연결된 다른 인접한 노드들을 확인
            for (int i = 0; i < graph.get(now).size(); i++) {
                int cost = d[now] + graph.get(now).get(i).getDistance();
                // 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
                if (cost < d[graph.get(now).get(i).getIndex()]) {
                    d[graph.get(now).get(i).getIndex()] = cost;
                    pq.offer(new Node(graph.get(now).get(i).getIndex(), cost));
                }
            }
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();
        start = sc.nextInt();

        // 그래프 초기화
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<Node>());
        }

        // 모든 간선 정보를 입력받기
        for (int i = 0; i < m; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
            graph.get(a).add(new Node(b, c));
        }

        // 최단 거리 테이블을 모두 무한으로 초기화
        Arrays.fill(d, INF);

        // 다익스트라 알고리즘을 수행
        dijkstra(start);

        // 모든 노드로 가기 위한 최단 거리를 출력
        for (int i = 1; i <= n; i++) {
            // 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
            if (d[i] == INF) {
                System.out.println("INFINITY");
            }
            // 도달할 수 있는 경우 거리를 출력
            else {
                System.out.println(d[i]);
            }
        }
    }
}

면접에서 나올 수 있는 질문​

  • 다익스트라 알고리즘의 로직 설명
  • 기본적인 다익스트라 알고리즘 성능 개선하는 방법

참고​

기여자​


Junho Moon
📦