DFS와BFS

DFS와 BFS

DFS와 BFS는 그래프를 탐색하는 대표적인 두가지 방법이다. 이 두 가지 알고리즘에 대해 알아보기 전에 그래프에 대한 개념을 충분히 익히길 바란다. 그래프에 대한 개념이 충분히 있다고 가정하고 이 챕터를 소개하도록 하겠다.

DFS

DFS는 Depth-First Search의 약자로, 깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.

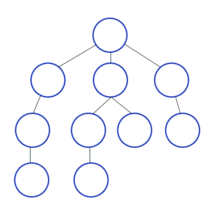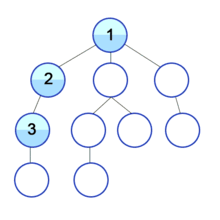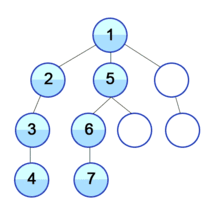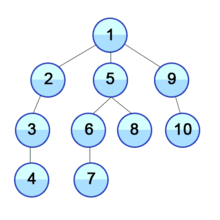
위와 같은 그림으로 그래프를 탐색하는 방식을 dfs라고 하며, 자세히 들여다 보면 트리의 깊이를 우선으로 탐색하는 것을 볼 수 있다.

dfs 시뮬레이션을 돌려보는 것도 좋은 예시가 될 수 있다.

DFS 구현 방법

dfs는 스택 자료구조에 기초하여 구현이 상당히 간단하다는 장점이 있다. 구현 순서는 다음과 같다.

1. 시작하는 칸을 스택에 넣고 방문했다는 표시를 남김
2. 스택에서 원소를 꺼내어 그 칸과 인접한 노드에 대해 3번을 진행
3. 해당 칸을 이전에 방문했다면 아무 것도 하지 않고, 처음으로 방문했다면 방문했다는 표시를 남기고 해당 칸을 스택에 삽입
4. 스택이 빌 때 까지 2번을 반복

이 때 모든 칸이 스택에 1번씩 들어가게 되므로 시간복잡도는 칸이 N개일 때 O(N) 이라고 볼 수 있다.

위의 과정을 파이썬으로 구현하면 다음과 같다.

def dfs(graph, v, visited):
    # 현재 노드를 방문 처리
    visited[v] = True
    print(v, end=" ")
    # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)

# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [[], [2, 3, 8,], [1, 7],[1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8], [1, 7]]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9

# 정의된 DFS 함수 호출
dfs(graph,1,visited)

# 답
1 2 7 6 8 3 4 5

DFS 장단점

• 장점

  • 현재 경로의 노드만을 기억하면 되어서 저장공간이 많이 필요하지 않다.
  • 찾고자 하는 노드가 깊은 단계에 있을 경우 빠르게 해를 구할 수 있다.
  • 최선의 경우, 가장 빠른 알고리즘이다. ‘운 좋게’ 항상 해에 도달하는 올바른 경로를 선택한다면, 깊이 우선 탐색이 최소 실행시간에 해를 찾는다.

• 단점

  • 찾은 해가 최적이 아닐 가능성이 있다.
  • 최악의 경우, 가능한 모든 경로를 탐험하고서야 해를 찾으므로, 해에 도달하는 데 가장 오랜 시간이 걸린다.

BFS

BFS는 Breadth First Search의 약자로 너비 우선 탐색이라는 의미를 갖는다. 쉽게 말해 가까운 노드부터 탐색하는 알고리즘이다.

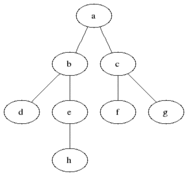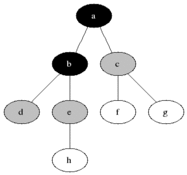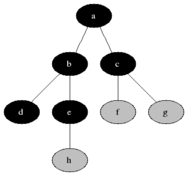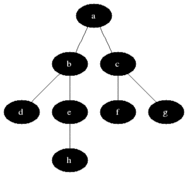
위와 같이 가까운 노드부터 탐색하는 것을 볼 수 있다.

bfs 시뮬레이션을 돌려보는 것도 좋은 예시가 될 수 있다.

BFS 구현 방법

bfs는 dfs와 달리 큐 자료구조를 활용하여 구현한다.

BFS의 시간복잡도를 생각해보면 방문 표시를 남기기 때문에 모든 칸은 큐에 1번씩만 들어가게 된다. 그렇기 때문에 시간복잡도는 칸이 N개일 때 O(N)이 된다.

BFS 구현의 자세한 순서는 다음과 같다.

1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.

이를 파이썬으로 표현하면 다음과 같다.

from collections import deque

# BFS 메서드 정의
def bfs(graph, start, visited):
    # 큐 구현을 위해 deque 라이브러리 사용
    queue = deque([start])
    # 현재 노드를 방문 처리
    visited[start] = True
    # 큐가 빌 때까지 반복
    while queue:
        # 큐에서 하나의 원소를 뽑아 출력
        v = queue.popleft()
        print(v, end=" ")
        # 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
        for i in graph[v]:
            if not visited[i]:
                queue.append(i)
                visited[i] = True

# 각 노드가 연결된 정보를 리스트 자료형으로 표현
graph = [[], [2, 3, 8], [1, 7], [1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8],[1, 7]]

# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9

# 정의된 BFS 함수 호출
bfs(graph, 1, visited)

# 답
1 2 3 8 7 4 5 6

BFS 장단점

• 장점
  • 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다.
• 단점
  • 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
  • 해가 존재하지 않는다면 유한 그래프(finite graph)의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다.
  • 무한 그래프(infinite graph)의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다.

언제 DFS를 쓰고 언제 BFS를 쓰는게 좋을까?

• 그렇게 깊지 않고 해답이 트리의 뿌리에서 그닥 떨어져 있지 않다는걸 알면 BFS를 쓰는 것이 좋다.
• 트리의 깊이가 상당히 깊은데 해답이 몇 개 없다면 DFS를 사용하는 방법은 깊이를 전부 다 서치하므로 시간이 엄청나게 걸릴거라 BFS가 낫다.
• 트리가 깊다기보다 엄청나게 넓으면 BFS의 사용은 메모리를 상당히 잡아먹을 것이다. 때문에, BFS의 사용은 실용적이지 못할 것이다.
• 해답들이 많지만 트리의 깊숙한 곳에 있다면 BFS는 실용적이지 못할 것이다.
• 트리가 엄청 깊으면 깊이를 제한하는 것도 필요할 것이다.

실제 알고리즘 풀이 유형

1. 그래프의 모든 정점을 방문하는 것이 주요한 문제 :

   단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용해도 상관없음.

2. 경로의 특징을 저장해둬야 하는 문제 :

   예를 들면 각 정점에 숫자가 적혀있고, a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용한다. (BFS는 경로의 특징을 가지지 못한다)

3. 최단거리 구해야 하는 문제 :

   미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리하다. 왜냐하면 dfs로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만, bfs로 현재 노드에서 가까운 곳부터 찾기 때문에 경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문이다.

4. 검색 대상 그래프가 정말 크다면 DFS를 고려한다.

5. 검색대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS를 쓴다.

DFS & BFS 연습문제

• 백준 - 깊이 우선 탐색
• 백준 - 너비 우선 탐색

나올 수 있는 면접 질문

• bfs 와 dfs란 무엇인가요?
• 두 알고리즘의 차이점은 무엇인가요?
• bfs와 dfs의 시간복잡도는 무엇이고 그 이유는 무엇인가요?
• bfs와 dfs의 장단점에는 무엇이 있나요?

참고

• 이것이 취업을 위한 코딩테스트다 with 파이썬
• 바킹독 알고리즘 블로그 - DFS
• 위키백과 - 깊이 우선 탐색
• 튜나 개발일기 - dfs & bfs

기여자

_{Kyun Heo}
📦